Der bekannte Physiker Cumrun Vafa stellt in „Das Universum in Rätseln“ die moderne Physik in all ihren Facetten dar: Er vermittelt faszinierende Erkenntnisse aus Kosmologie, Quantenphysik und Stringtheorie – mit Hilfe von Denksportaufgaben. Hier bist du gefragt: Kannst du die Probleme selbst lösen? Falls nicht, haben wir für dich auch die Lösungen parat.
Mehr Rätsel findest du im Buch: „Das Universum in Rätseln“ von Cumrun Vafa, ISBN 978-3-527-41406-2, erhältlich ab Dezember 2021.
Rätsel 1
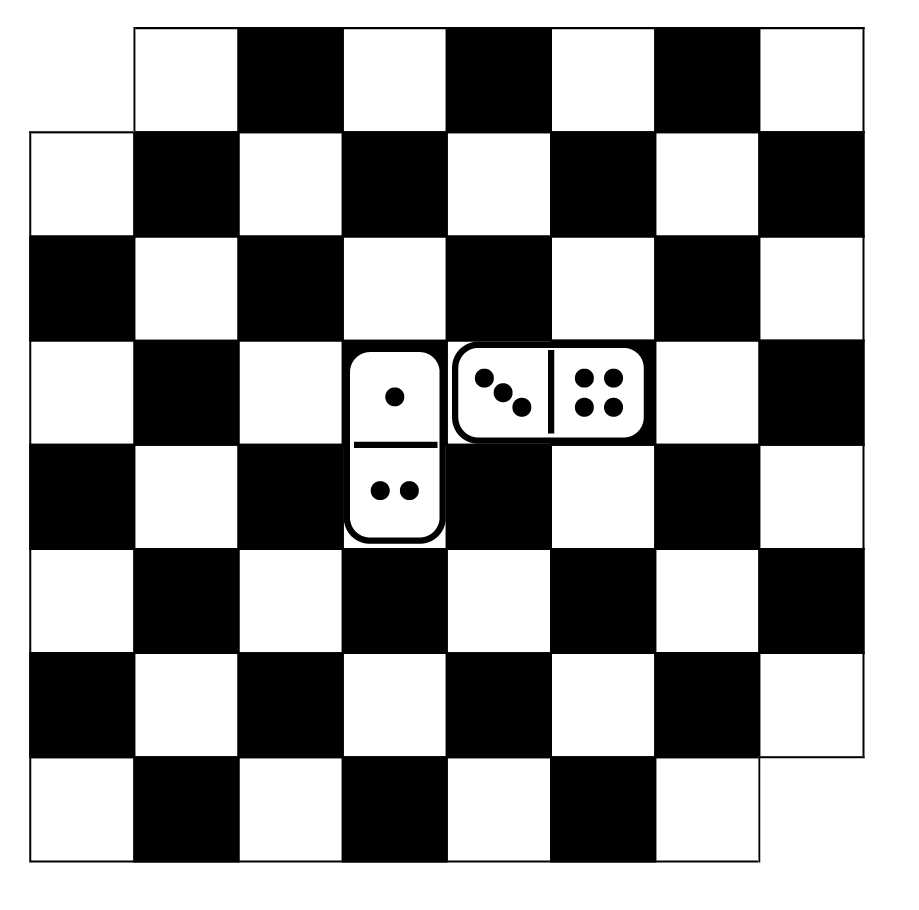
Sie haben ein gewöhnliches Schachbrett mit 64 Feldern vor sich, das Sie mit Dominosteinen bedecken sollen. Ein Dominostein deckt immer zwei benachbarte Felder ab. Der Haken an der Sache ist, dass Sie nur 31 Dominosteine zur Verfügung haben, sodass am Ende zwei Felder unbedeckt bleiben müssen (Abb. 1). Schaffen Sie es, die Dominosteine so zu legen, dass sie alle Felder bis auf zwei einander diagonal gegenüberliegenden Ecken des Bretts bedecken?
Rätsel 2
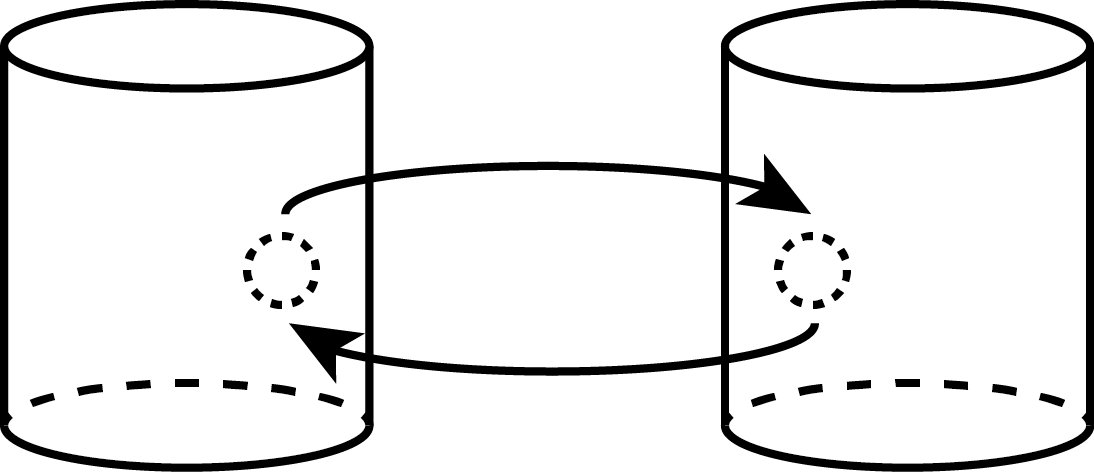
Sie haben zwei Behälter, in denen sich grüne bzw. weiße Farbe befinden. Beide Behälter sind gleich groß und enthalten genau die gleiche Menge Farbe. Angenommen, Sie schöpfen eine kleine Menge grüner Farbe aus dem einen Behälter und geben sie in den Behälter mit der weißen Farbe. Anschließend rühren Sie gut um und schöpfen dieselbe Menge Farbe aus dem Behälter mit der Mischfarbe und geben sie wieder zurück in den Behälter mit der grünen Farbe (Abb. 2). Ist nun die Konzentration der grünen Farbe im Behälter mit der weißen Farbe oder die Konzentration der weißen Farbe im Behälter mit der grünen Farbe größer?
Rätsel 3
Wir wollen uns nun ein etwas anspruchsvolleres Rätsel vornehmen. Wir betrachten dazu ein unendliches Gitter aus Quadraten im ersten Quadranten (der oberen rechten Ecke) eines normalen kartesischen Koordinatensystems.
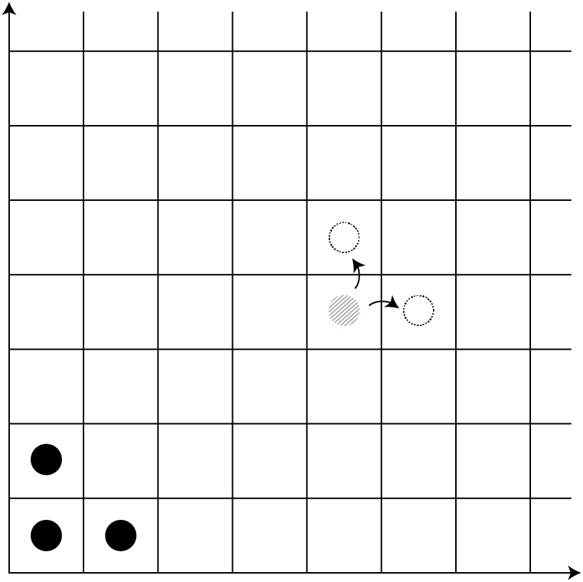
Wir platzieren Spielfiguren auf einige der Felder, die Sie nach einer bestimmten Regel verändern dürfen: Jede Figur kann durch zwei neue Figuren ersetzt werden, eine auf dem Feld direkt über und eine auf dem Feld unmittelbar rechts der vorhandenen Figur, sofern diese beiden Felder unbesetzt sind. Wir beginnen mit drei Spielsteinen auf den ersten drei Feldern in der linken unteren Ecke des Gitters, wie in Abb. 3 gezeigt. Sie sollen nun den beschriebenen Spielzug beliebig oft ausführen und so dafür sorgen, dass keine Spielsteine auf den drei Feldern links unten mehr übrig sind. Können Sie das mit einer endlichen Zahl von Spielzügen erreichen?
Rätsel 4
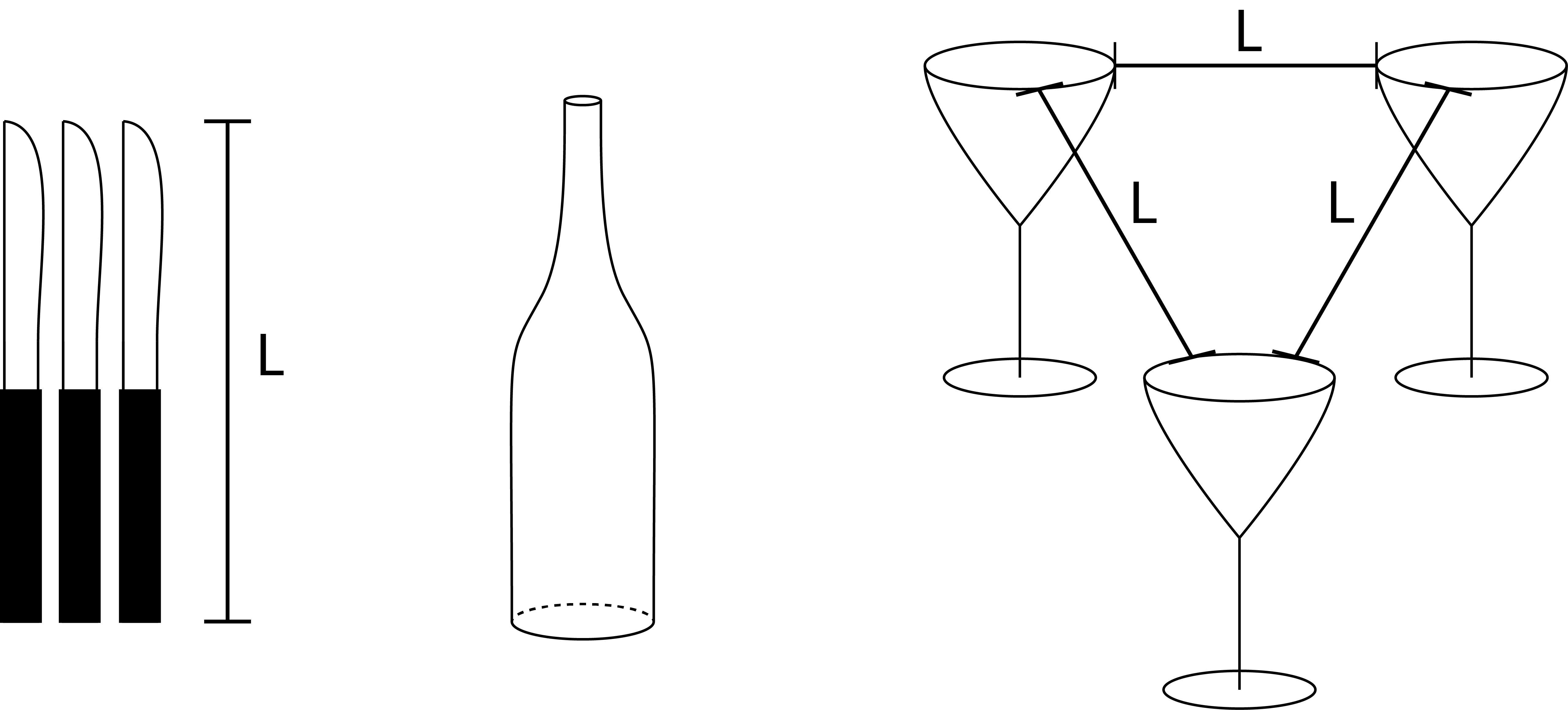
Sie haben drei Messer der Länge und drei Gläser, die in gleichen Abständen (etwas mehr als von Rand zu Rand) voneinander an den Ecken eines gleichseitigen Dreiecks aufgestellt sind (Abb. 4). Wie können Sie die Messer so anordnen, dass sie eine schwere Flasche auf den Gläsern abstützen können?
Rätsel 5
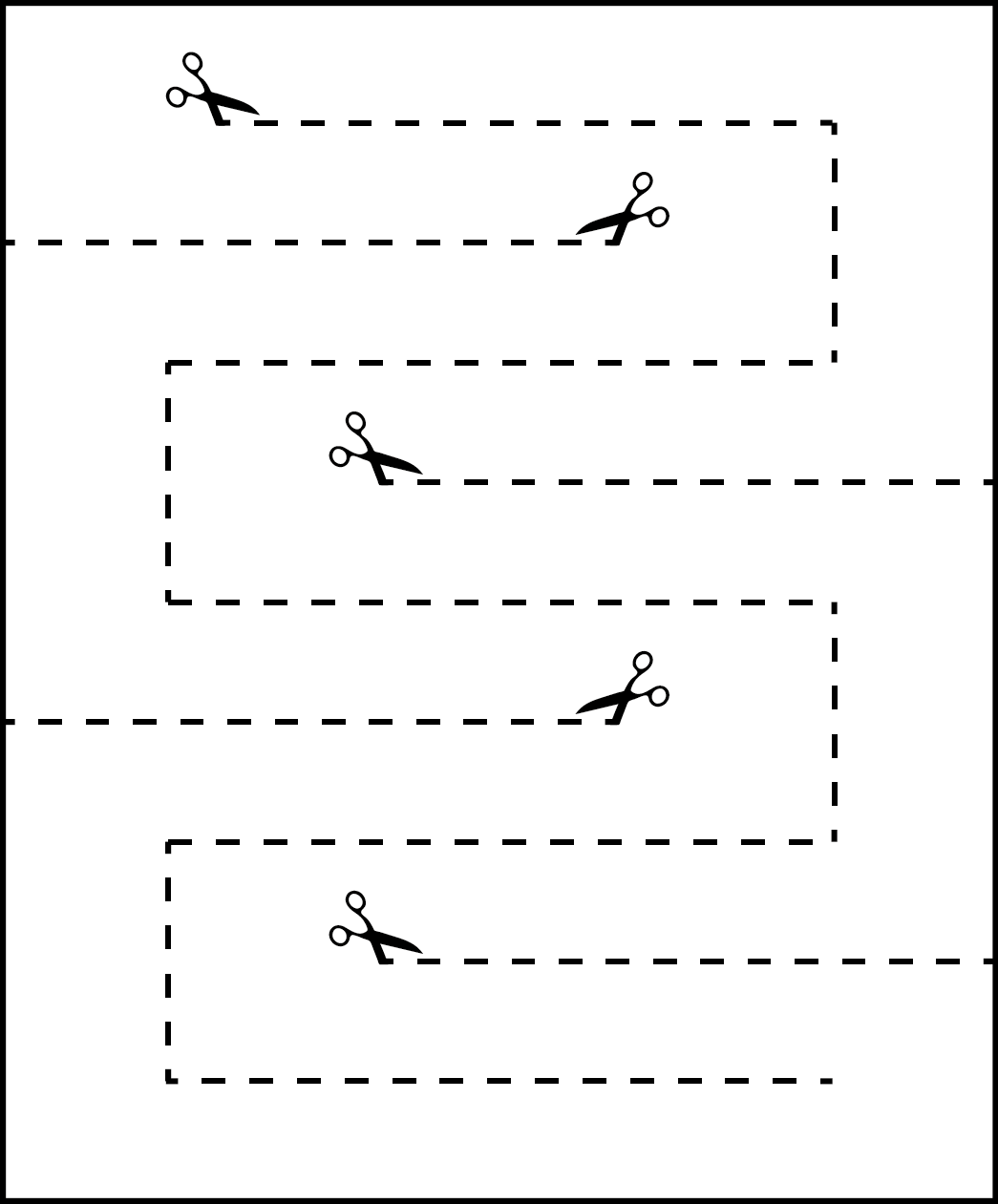
Sie bekommen ein Blatt Schreibpapier im Format A4 und eine Schere und sollen das Blatt so zerschneiden, dass es in einem Stück bleibt, aber Ihr ganzer Körper hindurchpasst. Ist das möglich?
Lösung Rätsel 1
Wenn Sie einen Dominostein auf das Schachbrett legen, deckt er immer ein schwarzes und ein benachbartes weißes Feld ab. Da zwei diagonal gegenüberliegende Ecken des Bretts aber immer dieselbe Farbe haben, ist die Aufgabe nicht lösbar. Dies ist ein Beispiel für einen Erhaltungssatz.
Wenn N schwarz und N weiß die Zahlen der schwarzen bzw. weißen Felder bezeichnen, die nicht bedeckt sind, dann ändern sich zwar N schwarz und N weiß, während Sie das Brett mit Dominosteinen bedecken, aber die Differenz Δ=N schwarz – N weiß bleibt immer gleich, weil jeder Dominostein genau ein schwarzes und ein weißes Quadrat abdeckt. Mit anderen Worten: Δ ist eine Erhaltungsgröße, die immer konstant bleibt und sich im Laufe der Zeit nicht verändert.
Angenommen, es wäre Ihnen gelungen, die Aufgabe wie gewünscht zu erfüllen, dann hätten Sie am Ende einen Zustand mit Δ=2 erreicht. Da Sie aber von einem Zustand mit Δ=32-32=0 ausgegangen waren, bevor Sie den ersten Dominostein gelegt hatten, müssen Sie diese Größe während des Auslegens der Steine irgendwie verändert haben. Da diese Differenz aber andererseits eine Erhaltungsgröße ist, die sich nicht ändern kann, haben wir einen Widerspruch vorliegen. Mit anderen Worten – wenn Sie nicht schummeln, gibt es keine Lösung für die Aufgabe, so wie sie gestellt wurde.
Lösung Rätsel 2
Die Konzentrationen müssen am Ende gleich sein! Da die Gesamtvolumina beider Farben am Anfang gleich waren, haben wir auch am Ende in jedem Behälter dasselbe Volumen. Aus der Erhaltung des Volumens der Farben ergibt sich daher, dass am Ende dieses Prozesses jedes Volumen grüner Farbe, das aus dem grünen Behälter verdrängt wurde, nur durch ein gleiches Volumen weißer Farbe ersetzt worden sein kann. Folglich ist die Menge an grüner Farbe, die in dem grünen Behälter nun fehlt, gleich der Menge an weißer Farbe, die in dem weißen Behälter fehlt. Die Mischung hat somit am Ende in beiden Behältern dieselben Konzentrationen. Das ist eine einfache, aber schöne Illustration für die Nützlichkeit von Erhaltungssätzen.
Der Grundgedanke hinter diesem Rätsel lässt sich auch anhand eines Kartenspiels veranschaulichen. Wir verwenden zehn rote und zehn schwarze Karten. Nun ziehen wir drei rote Karten aus der ersten Gruppe und mischen Sie sie mit den schwarzen Karten. Nach dem Mischen ziehen wir aus diesem gemischten Stapel von dreizehn Karten drei Karten und legen Sie sie zurück auf den roten Stapel. Überzeugen Sie sich selbst – in diesem Fall unter Verwendung der Erhaltung der Zahl der roten bzw. schwarzen Karten –, dass es nun in dem ursprünglich roten Stapel genauso viele schwarze Karten gibt und geben muss wie rote Karten in dem ursprünglich schwarzen Stapel.
Lösung Rätsel 3
Nein, das ist nicht möglich – jedenfalls nicht in einer endlichen Zahl von Zügen.
Um den Grund hierfür zu verstehen, weisen wir jedem Feld in diesem Gitter eine Zahl zu, sodass der numerische Wert eines Feldes gleich der Summe der beiden Felder direkt darüber und rechts davon ist. Genauer gesagt weisen wir dem ersten Quadrat in der linken unteren Ecke die Zahl 1 und den Feldern darüber und unmittelbar rechts davon jeweils die Zahl 1/2 zu; diese beiden Felder bilden die erste Diagonale. Die nächste Diagonale besteht aus drei Feldern, denen wir jeweils die Zahl 1/4 zuordnen. Die darauf folgende Diagonale besteht aus vier Quadraten, denen wir jeweils die Zahl 1/8 zuordnen usw. Mit jeder weiteren Diagonale halbieren wir die zugewiesene Zahl.
Nun addieren wir die Werte aller Felder, auf denen eine Figur steht. Wir stellen schnell fest, dass das Ersetzen einer Figur durch zwei neue Figuren gemäß Spielregel (eine um ein Feld nach rechts und eine um ein Feld nach oben versetzt) den Gesamtwert aller besetzten Felder nicht verändert. Für den Gesamtwert der von den Steinen besetzten Felder gilt also ein Erhaltungssatz. Der anfängliche Wert beträgt 1+1/2+1/2=2. Andererseits gilt für den Gesamtwert aller Felder (wenn also das gesamte Brett mit Figuren besetzt wäre)
[1+1/2+1/4+1/8+⋯]+1/2 [1+1/2+1/4+1/8+⋯]+1/4 [1+1/2+1/4+1/8+⋯]+⋯
=[1+1/2+1/4+1/8+⋯]×[1+1/2+1/4+1/8+⋯]=4 .
Da die anfänglich besetzten drei Felder zusammen einen Wert von zwei haben, muss die Summe aller besetzten Felder auch nach dem Entfernen der Figuren aus diesen drei Feldern entsprechend der Spielregel immer noch zwei betragen. Da aber der Gesamtwert aller unendlich vielen Felder (einschließlich der ersten drei) gerade vier beträgt, wie wir soeben gesehen haben, ist das nur dann möglich, wenn alle anderen (unendlich vielen) Felder des Gitters besetzt sind. Mit anderen Worten: die Aufgabe kann nicht in einer endlichen Anzahl von Schritten oder in einer endlichen Zeit erfüllt werden.
Lösung Rätsel 4
Um diese Aufgabe zu lösen, müssen Sie die Symmetrie der Anordnung brechen. Auf der in der Abbildung gezeigten Anordnung der Messer können Sie die Flasche auf dem dreieckigen Bereich in der Mitte abstellen.
Diese Anordnung führt eine Händigkeit in die Situation ein, die die ursprünglich vorhandene Symmetrie verletzt.

Lösung Rätsel 5
Intuitiv könnte man annehmen, dass das nicht gehen kann, da das Papier nur eine definierte Größe hat und nicht entscheidend vergrößert werden kann. Trotzdem ist die Aufgabe lösbar – zerschneiden Sie das Blatt entlang der in der Abbilung gezeigten Linien, sodass Sie anschließend durch den langen Papierstreifen hindurchsteigen können, den Sie erzeugt haben.