Perkolationstheorie oder: Das Bierdeckelspiel

Große Gebilde sind meist aus kleineren zusammengesetzt, mit einem Bauplan. So bestehen Häuser aus Bausteinen und Materie besteht aus Atomen, die wiederum aus einem Kern und diesen umkreisenden Elektronen. In diesen und einer Vielzahl ähnlicher Fälle gibt es klare Vorgaben, wie das Zusammenfügen zu geschehen hat. Bei der Perkolationstheorie wollen wir aber eine grundsätzlich andere Form von Verknüpfung betrachten: Wie können aus vielen gleichen Einzelteilen zusammenhängende Gebilde entstehen, wenn diese Einzelteile vollkommen willkürlich verteilt werden, zusammengewürfelt ohne irgendeinen Plan? Gibt es da doch noch zuständige Gesetze?

Perkolation von Bierdeckeln

Wir nehmen einen quadratischen Tisch mit einer Fläche von einem Quadratmeter und werfen auf diesen Tisch willkürlich runde Bierdeckel, die ihrerseits eine Fläche von 100 cm2 haben, also einen Radius von knapp 6 Zentimetern (s. Abbildung 1). Es macht nichts, dass dabei Deckel teilweise aufeinander zu liegen kommen. Im folgenden Bild sind einige sukzessive so erzeugte Konfigurationen dargestellt: neben einzelnen Deckeln findet man Inseln aus mehreren Deckeln, und mit zunehmender Deckelzahl werden die Inseln immer mehr und immer größer. Und irgendwann, beim Wurf noch eines weiteren Deckels gibt es plötzlich eine Insel, die von der einen Tischseite zur anderen reicht. Daneben gibt es noch kleinere, aber diese eine verbindet nun die gegenüberliegenden Tischseiten miteinander.  Wie viele Deckel muss man werfen, damit das geschieht? Die Anzahl variiert natürlich von Spiel zu Spiel immer ein wenig, aber wenn wir über viele Spiele mitteln, erfahren wir aus der dafür zuständigen mathematischen Theorie bei den vorgegebenen Tisch- und Deckelgrößen, dass dann die Seitenverbindung, das Einsetzen von Zusammenhang, bei etwa 110 Deckeln passiert. Die Summe aller Deckel ergibt somit eine Gesamtfläche, die etwas größer ist als die des Tisches: das liegt wiederum daran, dass die Deckel teilweise aufeinander liegen, sodass auch jetzt noch etwas „Luft“ bleibt.

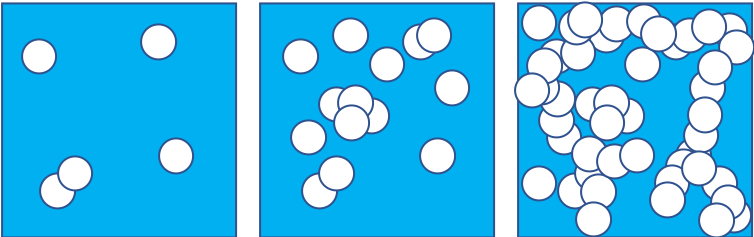
Perkolation, Abbildung 1: Sukzessive Anhäufung von Bierdeckeln auf einem Tisch

Perkolationstheorie

Mathematiker und Physiker nennen ein solch plötzliches Einsetzen einer Verbindung Perkolation. In der Perkolationstheorie untersucht man, wie aus vielen gleichen, völlig willkürlich angeordneten Einzelteilen ganz plötzlich ein zusammenhängendes Gebilde entstehen kann. Am Übergangspunkt sind somit schlagartig auch beliebig weit entfernte Teile miteinander verbunden. Die Perkolationstheorie ist heute ein aktuelles und äußerst vielseitiges Gebiet, mit Anwendungen, die von Schmelzprozessen und Netzwerkschaltung über Waldbrände bis hin zur Entstehung von Galaxien reichen.

Der Begriff Perkolation

Übrigens: Der Begriff Perkolation kommt aus der Kaffeezubereitung, bei der man Wasser in einen mit gemahlenem Kaffee gefüllten Filter gießt. Zunächst geschieht nichts, aber dann, plötzlich, bei einer ganz bestimmten Wassermenge, entsteht Durchfluss, es fließt Kaffee aus. Es ist eben dieser Durchfluss, den man als Perkolation bezeichnet, und in Amerika heißt die Kaffeemaschine deshalb auch Perkolator.

Etwas ganz Ähnliches geschieht beim Blumengießen: Erst versickert das hinzukommende Wasser, und dann plötzlich fließt es unten aus dem Topf heraus. Das Überraschende an diesen Vorgängen ist das plötzliche Einsetzen: Es fließen nicht erst einige Tröpfchen und dann immer mehr, sondern erst nichts und dann voller Fluss. 

Bei unserem Bierdeckelspiel ist das auch der Fall. Wenn wir das nach N Würfen von Bierdeckeln abgedeckte Gebiet mit der gesamten Tischfläche vergleichen, dann erhalten wir das folgende Bild. Zunächst steigt das Gebiet nur langsam an, da ja die Deckel einerseits mal hier, mal da, andererseits aber teilweise übereinanderliegen. Bis jetzt ist ein Großteil des Tisches noch leer. Aber sobald wir in die Nähe der kritischen Deckeldichte kommen, wächst das bedeckte Gebiet plötzlich rasant an und erreicht fast die Tischflächengröße. Mit noch weiter zunehmender Deckelzahl ist dann irgendwann der ganze Tisch bedeckt.

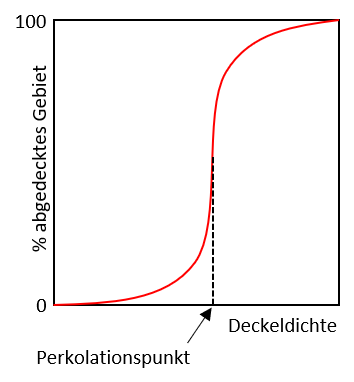
Perkolation, Abbildung 2: Anstieg der Flächendeckung mit Deckeldichte