Jeder, der ein Physikpraktikum durchlaufen muss, wird früher oder später mit der sogenannten Fehlerrechnung konfrontiert. Die Praktikumsassistenten und -assistentinnen legen sehr viel Wert darauf und werden jeden mit Punktabzug beim Praktikumsprotokoll sanktionieren, der keine Fehlerrechnung durchführt.
Absoluter Fehler = Größtfehler
Formal ist das Ganze ja ziemlich einfach: Es gibt eine Formel zur Abschätzung des absoluten oder Größtfehlers Δf einer Funktion f, die von n fehlerbehafteten Größen xi abhängt, f=(x1, …, xn),
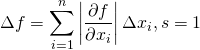
in die man die die Fehler Δxi der einzelnen Größen einsetzt. Doch was steckt eigentlich dahinter?
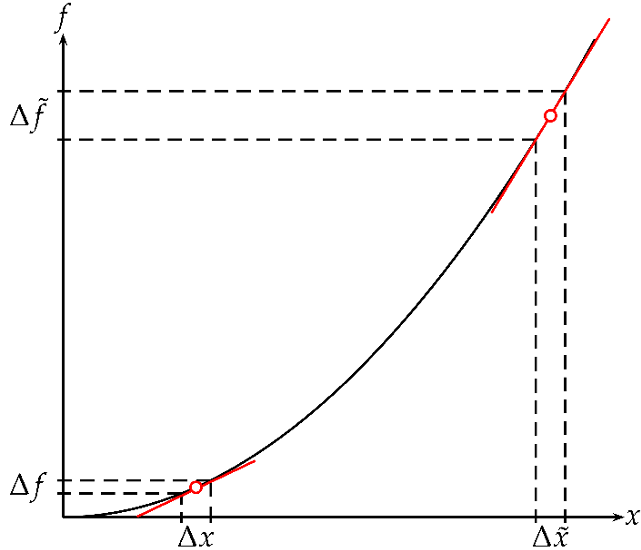
Der Einfachheit halber betrachten wir zunächst eine Funktion f, die nur von einer fehlerbehafteten Größe x abhängt; sie möge einen qualitativen Verlauf wie in der Abbildung haben, es könnte wohl irgendwas Parabolisches sein. Diese physikalische Größe f, die unser Modell ist, hängt also von der Größe x ab, die wir aus den verschiedensten Gründen nicht beliebig genau messen können, sondern immer nur mit einer Unsicherheit Δx. Aus der Abbildung wird ersichtlich, dass der im Funktionswert sich ergebende Fehler Δf offensichtlich davon abhängt, an welcher Stelle im Funktionsverlauf wir uns befinden (Frage: Für welche Funktion gilt das nicht?): weit vorne ist der aus Δx resultierende Fehler Δf klein, weiter hinter ist der aus ![]() resultierende Fehler
resultierende Fehler ![]() schon recht groß. Idealerweise gehen wir davon aus, dass der Messfehler Δx sehr klein gegenüber dem Messwert x ist. Sollte dies nicht der Fall sein, dann sollten wir unsere Messmethode überdenken. Ein Dezimetermaßstab etwa eignet sich sicher nicht, um den Durchmesser eines dünnen Kupferrohres zu messen, der in der Größenordnung 5 mm liegt.
schon recht groß. Idealerweise gehen wir davon aus, dass der Messfehler Δx sehr klein gegenüber dem Messwert x ist. Sollte dies nicht der Fall sein, dann sollten wir unsere Messmethode überdenken. Ein Dezimetermaßstab etwa eignet sich sicher nicht, um den Durchmesser eines dünnen Kupferrohres zu messen, der in der Größenordnung 5 mm liegt.
Bei einem hinreichend kleinen Δx und einer sich hinreichend wohlverhaltenden Funktion f jedoch können wir deren Funktionsverlauf im Intervall Δx ohne allzu großen Fehler durch ein Geradenstück approximieren (Übung für Fortgeschrittene: Wie lässt sich der Ausdruck „ohne allzu großen Fehler“ quantifizieren?). Die Näherung einer Funktion in einer kleinen Umgebung einer Stelle x durch ein Geradenstück ist nun gerade der Kern der Differentialrechnung, die uns lehrt, dass die Steigung der Tangente in einem Punkt gegeben ist durch den Wert der ersten Ableitung in diesem Punkt.
Damit können wir schlussfolgern: Der Fehler Δf ist umso größer, je größer die Steigung der Tangente im betrachteten Intervall Δx ist. In endlichen Intervallen ist die Steigung gegeben durch m = Δf / Δx, Stichwort Steigungsdreieck. Wir stellen uns Δx sehr klein vor und schicken es idealisierend gegen Null, und das ist nichts anderes als die Ableitung:
![]()
Wir kombinieren also zwei fundamental verschiedene Sachverhalte: der Einfluss eines realen Fehlers Δx auf eine Größe Δf wird bestimmt durch eine idealisierte infinitesimale Änderung dieser Funktion f, die Ableitung. Ableitungen können bekanntlich auch negativ sein: da wir den Größtfehler suchen, setzen wir noch Betragsstriche um die Ableitung und voilà: wir haben die eingangs erwähnte Formel für den Größtfehler für den Fall hergeleitet, dass f nur von einer fehlerbehafteten Größe abhängt.
Die Verallgemeinerung auf n fehlerbehaftete Größen liegt auf der Hand, wir summieren einfach die einzelnen Größtfehler auf.
Relativer Fehler
Falls die Funktion f nur in Form von Produkten oder Quotienten von den fehlerbehafteten xi abhängt, gilt eine vereinfachte Regel zur Berechnung des resultierenden relativen Fehlers. Sie ergibt sich als Spezialfall der eingangs erwähnten Formel, angewandt auf die Funktion
![]()
Da die αi auch negativ sein können, ist auch der Fall abgedeckt, dass Quotienten auftreten, denn x–α=1/xα. Die partielle Ableitung nach einem xi lautet:
![]()
und somit der resultierende Größtfehler
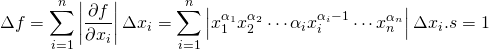
Dieser Ausdruck wird durch ![]() dividiert, dabei kürzt sich auf der rechten Seite in jedem Summanden fast alles raus.
dividiert, dabei kürzt sich auf der rechten Seite in jedem Summanden fast alles raus.
Es verbleibt
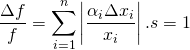
© Martin Preuß