Bézier-Kurven und Karosseriedesign

Bézier-Kurven/Abbildung 1 Citroën DS

Was hat dieses Auto mit Bézier-Kurven zu tun? Bis in die späten 1950er-Jahre haben Karosseriedesigner Tonmodelle von Autos angefertigt, doch mit der zunehmenden Mechanisierung und Automatisierung des Autobaus mussten Methoden gefunden werden, Kurven und Flächen mathematisch zu beschreiben und zu modellieren. Eine elegante Lösung für das Problem haben, mehr oder weniger zeitgleich, die Karosseriedesigner bei Renault (Bézier) und bei Citroën (de Casteljau) entwickelt.

Bézier-Kurven sind spezielle parametrische Kurven, die seit den 1960er-Jahren im Karosseriedesign und in neuerer Zeit im CAD-/CAM-Bereich und in der Computergrafik weite Verbreitung gefunden haben, weil sie einfach, anschaulich, flexibel und numerisch gut beherrschbar sind. Diese Kurven wurden unabhängig voneinander von de Casteljau bei Citroën (1959) und von Bézier bei Renault (1961) entdeckt wurden, wobei ersterer zur Geheimhaltung verpflichtet war, letzterer nicht. Im Allgemeinen spricht man daher von Bézier-Kurven, hat aber auch Herrn de Casteljau nicht vergessen, nach dem der numerisch stabilste Algorithmus zur Implementierung benannt ist.

Wenn man Bézier-Kurven im Detail verstehen möchte, kommt man um eine Menge (einfache, aber fisselige) Mathematik nicht herum. Wir beschränken uns hier daher auf die grundlegenden Ansätze sowie Bézier-Kurven im zweidimensionalen Raum.

Ausgangspunkt ist:

Bézier-Kurven kann man als das Ergebnis einer verallgemeinerten linearen Interpolation zwischen Punkten im zweidimensionalen Raum auffassen.

„Bézier-Kurven“ ersten Grades

Wir betrachten zur Einstimmung die einfache lineare Interpolation zwischen zwei Punkten A₀ und A₁, siehe Abbildung 2. Wenn wir einen Parameter t einführen, der zwischen 0 und 1 variieren kann, ergibt sich jeder Punkt X(t) auf der Strecke zwischen A0 und A1 durch

X(t)=(1–t)·A₀+t·A₁

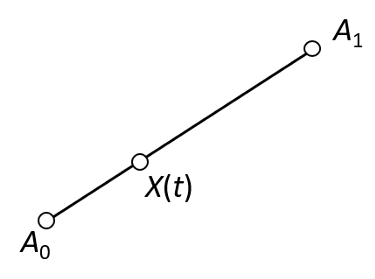
Abbildung 2: Lineare Interpolation zwischen zwei Punkten

Reality check: Für t=0 ist X=A₀, für t=1 ist X=A₁. Das Ganze ist natürlich nicht besonders spannend, denn X(t) ist nur eine gerade Strecke. Aber, wenn man will, kann man den obigen Ausdruck schon als Bézier-Kurve bezeichnen, und zwar als Bézier-Kurve ersten Grades.

Bézier-Kurve zweiten Grades

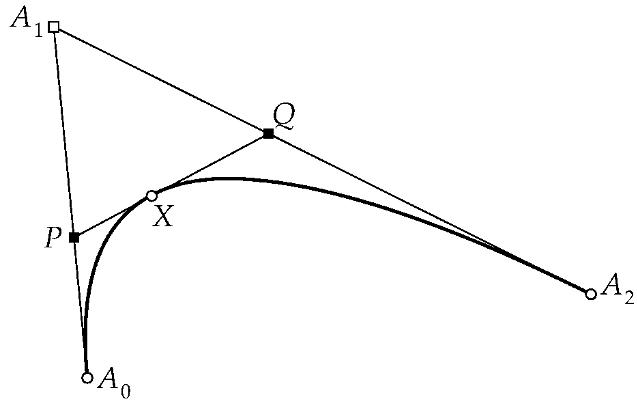
Abbildung 3: Beispiel einer Bézier-Kurve zweiten Grades mit Anfangs- und Endpunkt A₀ und A₂ sowie Einflusspunkt A₁

Wesentlich interessanter wird die Sache, wenn wir drei Punkte A₀, A₁, A₂ betrachten. Wir konstruieren den Punkt P, indem wir zwischen A0 und A1 linear interpolieren, und den Punkt Q, indem wir zwischen A1 und A2 linear interpolieren. Schließlich konstruieren wir einen Punkt X als lineare Interpolation zwischen P und Q (Abbildung 3). Nach ein bisschen einfacher Rechnerei finden wir den Punkt X in Abhängigkeit von t als

X(t)=A₀· (1–t)²+A₁·2· (1–t) ·t+A₂·t².

Reality check: Für t=0 ist X=A₀, für t=1 ist X=A₂. Wer sich jetzt wundert, dass der Punkt A₁ nicht passiert wird: das ist konstruktionsbedingt gar nicht möglich. Der Punkt A₁ spielt vielmehr die Rolle eines Einflusspunktes, dessen Lage in der Ebene die Form und den Verlauf der Kurve beeinflusst, die A0 und A2 verbindet. Wer das interaktiv ausprobieren möchte, kann dies zum Beispiel im kostenlosen Tool Geogebra tun.

Die Gleichung zur Bestimmung von X ist quadratisch in t, daher heißen die so erhaltenen Bézier-Kurven naheliegenderweise Bézier-Kurven zweiten Grades. Sie werden zum Beispiel zur Beschreibung der Umrisse von TrueType-Schriften verwendet. Sie sind schon recht flexibel, aber noch nicht flexibel genug: So kann sich eine Bézier-Kurve zweiten Grades nicht schneiden.

Bézier-Kurven dritten Grades

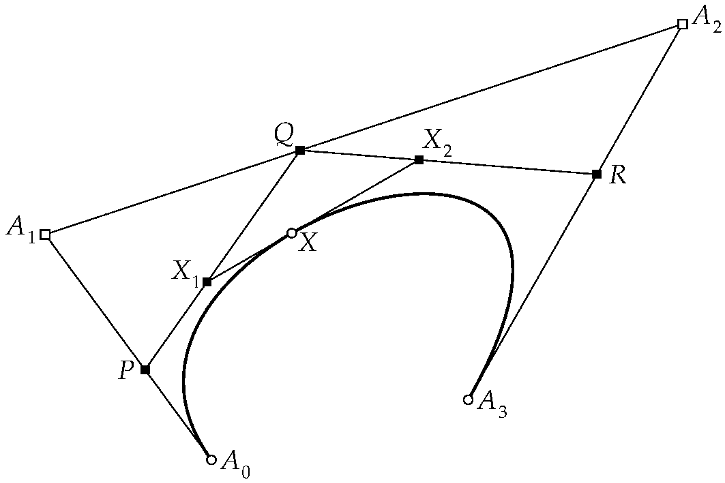
Abbildung 4: Beispiel einer Bézier-Kurve dritten Grades mit Anfangs- und Endpunkt A₀ und A₃ sowie Einflusspunkten A₁ und A₂

Da die Bézier-Kurven zweiten Grades zu beschränkt waren, haben sich für die Anforderungen der Praxis Bézier-Kurven dritten Grades durchgesetzt. Das Prinzip ist das gleiche wie vorher, nur haben wir jetzt vier Punkte A0, A1, A2, A3 und damit einen Einflusspunkt mehr, der Form und Verlauf der resultierenden Kurve zwischen A0 und A3 beeinflusst. Wir bestimmen (Abbildung 4):

• P durch Interpolation zwischen A₀ und A₁
• Q durch Interpolation zwischen A₁ und A₂
• R durch Interpolation zwischen A₂ und A₃
• X₁ durch Interpolation zwischen P und Q
• X₂ durch Interpolation zwischen Q und R
• X durch Interpolation zwischen X₁ und X₂

Die Rechnungen werden nun etwas unübersichtlicher, aber nicht konzeptionell schwieriger; im Ergebnis ergibt sich der Punkt X zu

X(t)=A₀· (1–t)³+A₁·3· (1–t)²·t+A₂·3· (1–t) ·t²+A₃·t³.

Man kann das Spiel noch weitertreiben und Bézier-Kurven mit mehr Einflusspunkten betrachten, was aus mathematischer Sicht höchst spannend ist, für die Praxis aber keine so große Rolle mehr spielt. Als Ausblick sei noch erwähnt, dass Bézier-Kurven dritten Grades die Basis sind für die sogenannten kubischen Splines: diese sind nichts anderes als nach bestimmten Kriterien miteinander verbundene Bézier-Kurven dritten Grades.

Bücher zur Mathematik in den Naturwissenschaften