Die Kettenlinie

Befestigt man eine Kette oder ein Seil an zwei Punkten, so stellt sich unter dem Einfluss der Schwerkraft eine Form wie in der Abbildung ein. Und nein, es ist keine Parabel.

Herleitung des analytischen Ausdrucks der Kettenlinie
Die an einem Punkt der Kette tangential wirkende Kraft aufgrund der Schwerkraft wird zerlegt in einen horizontalen Anteil $F_\mathrm{h}$ und einen vertikalen Anteil $F_\mathrm{v}$ , siehe Skizze.

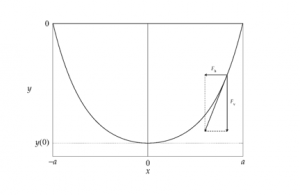
In jedem Punkt der Kette gilt demzufolge $F_\mathrm{v}=F_\mathrm{h}y'$ . Die horizontale Komponente entspricht der (negativen) Spannung der Kette, die aus der Masse der Kette und der Tatsache resultiert, dass diese an zwei Aufhängepunkten befestigt ist. Sind Lage der Aufhängepunkte sowie die Masse konstant, so muß auch die Horizontalkomponente der wirkenden Kraft konstant sein, wir können also folgern
$\displaystyle\frac{\mathrm{d}F_\mathrm{v}}{\mathrm{d}x}=F_\mathrm{h}y''.$

Wenn wir von einer homogen mit Masse der Dichte $\varrho$ belegten, eindimensionalen Kette ausgehen, ergibt sich das Massenelement $\mathrm{d}{m}$ , das der Schwerkraft in $y$ -Richtung unterliegt, zu
$\mathrm{d}{m}=\varrho\,\mathrm{d}{s}=\varrho\sqrt{\mathrm{d}x^2+\mathrm{d}y^2}=\varrho\sqrt{1+(y')^2}\,\mathrm{d}{x},$
so dass wir für die Vertikalkomponente der Kraft erhalten:
$\mathrm{d}F_\mathrm{v}=g\,\mathrm{d}m=g\varrho\sqrt{1+(y')^2}\,\mathrm{d}x.$

Nach Division durch $\mathrm{d}{x}$ und unter Berücksichtigung von $\mathrm{d}F_\mathrm{v}/\mathrm{d}x=F_\mathrm{h}y''$ ergibt sich daraus
$\displaystyle\frac{\mathrm{d}F_\mathrm{v}}{\mathrm{d}x}=g\varrho\sqrt{1+(y')^2}=F_\mathrm{h}y'',$
also mit $k=g\varrho/F_\mathrm{h}$ die nichtlineare homogene Differentialgleichung zweiter Ordnung
$y''=k\sqrt{1+(y')^2}.$

Diese Differentialgleichung hat als allgemeine Lösung den Cosinus Hyperbolicus in der Form
$y=\displaystyle\frac{1}{k}\cosh{k(x+\alpha)}+\beta$
mit den Parametern $\alpha$ und $\beta$ , die durch die Randbedingungen bestimmt werden: Das Minimum dieser Funktion stellt sich ein für ein $x_0$ , das bestimmt wird durch $y'(x_0)=0$ , also $x_0=-\alpha$ . Im in der Abbildung dargestellten Fall ist aus Symmetriegründen $x_0=0$ , so dass wir erhalten:
$y=\displaystyle\frac{1}{k}\cosh{kx}+\beta.$

Fordern wir weiter, dass die Kette in den Punkten $(-a,0)$ und $(a,0)$ aufgehängt ist, was wir ohne Beschränkung der Allgemeinheit stets durch Verschiebung der $x$ -Achse des Koordinatensystems erreichen können, ergibt sich
$\displaystyle\frac{\cosh{ka}}{k}+\beta=0,\quad\text{also}\quad\beta=-\frac{\cosh{ka}}{k}.$

Damit erhalten wir den folgenden analytischen Ausdruck der Kettenlinie:
$\displaystyle y=a\cdot\frac{\cosh{kx}-\cosh{ka}}{ka}.$
Eine solche Kette hängt um $|y(0)|=\cosh{ka}/k$ durch.

Die Größe $k$ enthält aber gerade die kettenspezifischen Eigenschaften, abgesehen von Materialparametern insbesondere die als vorgegeben gedachte Länge $\ell$ .

Der Zusammenhang zwischen $\ell$ und $k$ ergibt sich vermöge
$\displaystyle\ell=\int_{-a}^a\mathrm{d}{s}=\int_{-a}^a\mathrm{d}x\;\sqrt{1+[y'(x)]^2}=\int_{-a}^a\mathrm{d}x\;\cosh{kx}=\frac{2\sinh{ka}}{k}.$